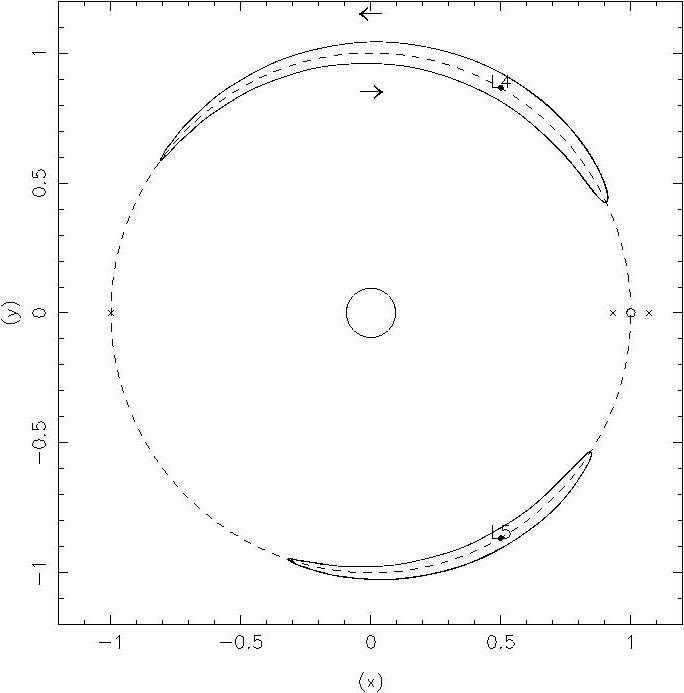



Este estudou o movimento de um asteróides sujeito à força gravitacional exercida pelo Sol e por um planeta, e mostrou que este problema tem cinco configurações de equilíbrio relativo (isto é, posições que o asteróides pode ocupar mantendo sempre a mesma distância em relação ao Sol e ao planeta). Quando observadas por um habitante do planeta (ou seja, a partir de um referencial em órbita com o planeta à volta do Sol), estas configurações correspondem a pontos fixos (os chamados pontos lagrangianos): dois destes (L4 e L5 na Fig. 1) ocupam os vértices de dois triângulos equiláteros cuja base comum é a distância do Sol ao planeta (estes dois corpos estão assinalados, respectivamente, com círculo pequeno e círculo grande na Fig. 1). Os outros três pontos lagrangianos são colineares com o Sol e o planeta e estão assinalados com x na Fig. 1.

Fig. 1 Esquema representando as posições do Sol (no centro) e de um planeta (indicado pelo círculo pequeno, à direita) em órbita circular em torno do Sol. Os pontos lagrangianos estáveis deste sistema estão assinalados como L4 e L5, enquanto que as cruzes indicam os outros pontos (instáveis) de Lagrange.O interesse astrofísico dos pontos lagrangianos reside no facto de estes serem pontos de equílibrio, logo são locais onde um asteróides permanecerá, à partida, indefinidamente. No entanto, na prática só será de esperar encontrar um asteróides na vizinhança de um ponto lagrangiano caso este seja estável (dado que também poderia ser um ponto de equilíbrio instável). É fácil de compreender porquê se imaginarmos uma bola colocada numa superfície como a da Fig. 2, onde A, B e C são, obviamente, pontos de equilíbrio. Se sujeitarmos a bola a uma perturbação, ela rolará dos cumes A e C (estes são pontos de equílibrio instáveis). No entanto, no caso do ponto B, se a perturbação for suficientemente pequena, a bola oscilará à volta de B (que é portanto um ponto de equílibrio estável, dentro de uma certa região de estabilidade limitada por A e C).
Lagrange mostrou que, enquanto que os pontos colineares são instáveis, L4 e L5 são estáveis, ou seja, existe uma certa região de estabilidade à volta de L4 e L5. Embora o tamanho desta possa ser muito pequeno, sabe-se, no entanto, hoje em dia, que existem órbitas que oscilam à volta de L4 ou L5 (as regiões finas desenhadas na Fig. 1) com amplitudes que podem atingir cerca de 150 graus, embora a prova teórica da estabilidade de regiões deste tamanho não esteja ainda estabelecida.
Até à data foram observados cerca de 600 asteróidess em órbitas na vizinhança de L4 e L5 de Júpiter, um grupo ao qual Aquiles pertence. Estes são conhecidos como os asteróidess Tróianos por terem sido baptizados com os nomes dos heróis da guerra mítica de Tróia. De momento é também conhecido um asteróides com uma órbita na vizinhança de L5 de Marte.
No que diz respeito aos outros planetas do Sistema Solar, a existência de asteróides deste tipo, com órbitas associadas a esses planetas, é ainda uma questão de debate.
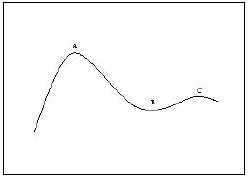
Fig. 2 Ilustração de casos de equilíbrio estável (B) e instável (A e C).Doutora Helena Morais


