O Observat\'orio -- {\large\bf A Busca de Vida Extraterrestre (III) }

Go backward to A Teoria da Relatividade e o GPS.
Go up to Top
Go forward to Para observar em Abril

A Busca de Vida Extraterrestre (III)

Na sequência dos números anteriores, vamos aqui analisar métodos adicionais de detecção de planetas extrasolares. Em particular, vamos abordar o problema da detecção através dos trânsitos de planetas (eclipse da estrela devido à passagem dum planeta em frente do disco estelar).

d) Trânsitos de planetas

No caso do plano da órbita do planeta estar correctamente orientado, por forma a que o planeta se interponha entre a estrela central e o observador, uma diminuição do brilho da estrela irá ocorrer durante o trânsito do planeta, como se ilustra na Figura 1: na posição 1, o brilho total que nos chega é o brilho da estrela mais o brilho do planeta (que resulta de luz da estrela reflectida na superfície deste); na posição 3, o brilho detectado corresponde ao brilho total da estrela menos o brilho correspondente à fracção da superfície da estrela cuja luz não nos chega, devido ao planeta em trânsito.

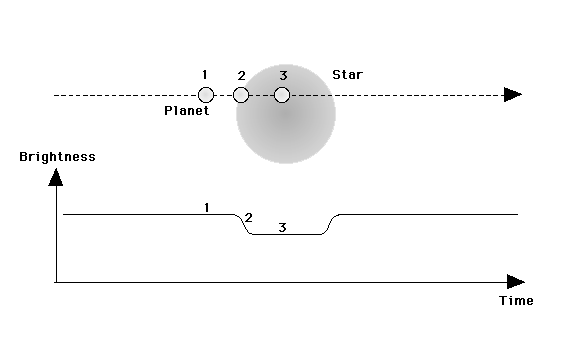
Fig. Trânsito de um planeta e respectiva curva de luz mostrando a variação do brilho da estrela em função do tempo.

A detecção de um trânsito através da análise da curva de luz da estrela requer que se verifiquem três condições, a saber:

O plano da órbita do planeta deve estar orientado correctamente: para orientações aleatórias, a probabilidade geométrica de que tal aconteça é dada por
p= $R$ _estrela/a
onde $R$ _estrela é o raio da estrela e $a$ o raio da órbita do planeta. Para um planeta como a Terra em torno de uma estrela com raio igual ao do Sol, esta probabilidade é apenas de $0.5%$ !! Para um planeta como Júpiter, esta probabilidade seria cinco vezes menor. Além disso, como a luz da estrela tem de ser continuamente medida por fotometria pelo menos ao longo de uma órbita completa do planeta, este método do trânsito torna-se pouco eficiente para grandes valores de $a$ , e favorece a detecção de planetas com órbitas pequenas (com pequenos valores de $a$ ), uma vez que nestes casos a probabilidade $p$ é maior e o tempo de monitorização é mais curto.
A duração do trânsito é dada por
Delta T=( $R$ _estrela/a)(P/ $Pi$ )
onde $P$ é o período da órbita do planeta. Para um planeta como a Terra, o trânsito duraria cerca de 13 horas, enquanto que para um planeta do tipo Joviano o trânsito seria de 25 horas. Ou seja, a duração do trânsito não é particularmente sensível ao raio da órbita do planeta.
O brilho relativo $Delta (F/F)$ provocado pelo trânsito do planeta é dado por
Delta (F/F)= $(R$ _P/R_estrela)²
onde $R$ _P é o raio do planeta. A precisão fotométrica na curva de luz da estrela observada deve ser melhor que $Delta (F/F)$ . Para um planeta com o raio da Terra, o brilho relativo é de apenas $10$ ^-4, ou seja dez mil vezes menor que o brilho da própria estrela.

Para observações efectuadas a partir do solo aqui na Terra, a precisão fotométrica actualmente conseguida é, no melhor dos casos, cerca de

0.1%

, ou seja

10

^-3, o que significa que estamos ainda uma ordem de grandeza abaixo do necessário. Contudo, no espaço podemos atingir precisões da ordem de

10

^-4 para estrelas de magnitude 15, com um telescópio de 50 cm e tempos de exposição de 1 hora. A missão COROT, um telescópio espacial de 27 cm de abertura a ser lançado em 2004, terá a capacidade de detectar planetas do tipo terrestre por este método. Para tal, será efectuada fotometria de cerca de 50 000 estrelas com magnitudes entre 11 e

15.5

no visível). A fotometria terá uma precisão entre

7×10

^-4 e

5×10

^-3 para integrações de cerca de 1 hora. Estes valores significam que a probabilidade de detectar trânsitos de planetas terrestres é baixa, mas esperam-se algumas detecções de planetas cujos raios sejam pelo menos 2 vezes o raio da Terra.

Dr. Miguel C. Moreira
CAAUL, Centro de Astronomia e Astrofísica da Universidade de Lisboa